You may be familiar with real numbers and their subtypes (rationals, irrationals, integers, etc.). If you need a refresher see “Real Numbers, From The Ground Up”. You may also know that there is an infinite number of real numbers and also an infinite number of each subtype of real numbers. And some of those infinities are equal to others (e.g. # integers = #rationals) while some are larger than others (# irrationals > # rationals). See “Number Of Numbers: Infinite Weirdness” for a discussion of the cardinality of real numbers. What you may not be too familiar with is that there is a more general concept of numbers. Numbers can be thought of as a set of elements on which you can do arithmetic. The mathematical name for such a set is a field. This article will introduce you to finite fields: sets of a finite number of elements with well-defined arithmetic on the elements. Such fields have myriad practical applications in cryptography, data integrity, data coding, etc.

Arithmetic On A Field

What exactly is arithmetic on a field of numbers which are merely elements in some set? For real numbers, we understand arithmetic in a geometric way on the real number line. For example, to add 1.2 to 3.5, you start at 3.5 on the number line and move a distance 1.2 rightward. But for an arbitrary field with possibly no such equivalent number line to invoke, we have to use an algebraic approach instead. In such a formulation, arithmetic consists of two operations on every pair of numbers. The operations are addition (denoted by the symbol ‘+’) and multiplication (denoted by the symbol ‘*’). Both these operations behave similarly to addition and multiplication on real numbers. This behavior consists of several properties like associativity, commutativity, distributivity, and so on, but let’s not get bogged down in too many technical details. The salient properties to understand the basics are the following:

1. Adding or multiplying any two numbers gives another number in the set.
2. “0” is a number in the set with the usual property that it can be added to any other number without changing that number.
3. Every number has an equivalent negative number in the set with the usual property that the sum of the two is “0”. Subtracting a number is then defined as adding the negative of that number.
4. “1” is a number in the set with the usual property that it can be multiplied with any other number in the set without changing that number.
5. Every number (except “0”) has an equivalent reciprocal number in the set with the usual property that the multiplication of the two is “1”. Dividing by a number is then defined as multiplying by the reciprocal of that number.

Let’s see which types of real numbers are fields, based on the above properties:

------------------------------------------------------------------
| Type | Field? | Why? |
------------------------------------------------------------------
| Reals | Yes | Satisfies all properties |
| Rationals | Yes | Satisfies all properties |
| Irrationals | No | 0 is not irrational |
| Integers | No | Reciprocals (e.g. 1/2) are not integers |
------------------------------------------------------------------

Prime Fields

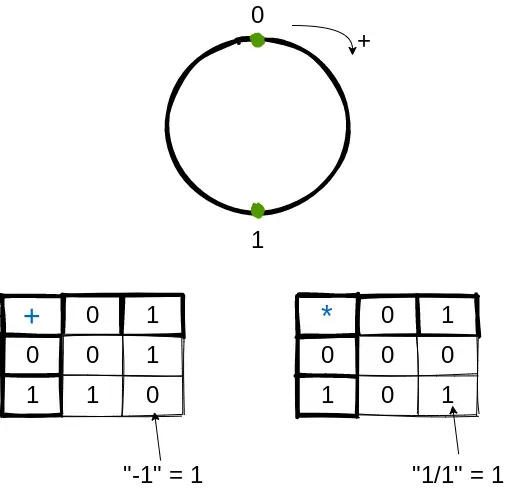
What is the smallest field? A field of the 2 numbers: 0 and 1. Let’s call this the 2-field. You can think of this field as 2 points on a numbered circle (e.g. 0 at 12 o’clock and 1 at 6 o’clock) with addition executed as clockwise hops. This is equivalent to performing all arithmetic operations like normal real numbers, dividing the normal result by 2, and using the remainder as the actual result. This way each result is a 0 or a 1 and is a member of the 2-field. Wouldn’t elementary school have been so much easier if we worked with 2-fields instead of the real numbers field?

Can the 2-field construction above be generalized to 3-field, 4-field, and so on for larger sized finite fields? Turns out that it only works for fields that have a prime number of numbers. So, a 3-field has the numbers 0, 1, 2. A 5-field has the numbers 0, 1, 2, 3, 4. And so on. For every prime number ‘p’ there is a p-field with ‘p’ numbers from 0 to p-1 and addition/multiplication performed as normal integers with the additional step of dividing the result by ‘p’ and using the remainder as the result.

Why doesn’t a composite number ‘c’ give us a c-field in the same way? One reason is that there is at least one number in the set that does not have an equivalent reciprocal number. For example, if ‘c’ is 4, then there is no number in the 4-field that multiplies with 2 to give 1 (2*0 = 0, 2*1 = 2, 2*2 = 4 -> 0, 2*3 = 6 -> 2). In general, every prime factor of ‘c’ is a non-zero element of the c-field with no reciprocal element in the field. Here’s the proof:

Extension Fields

Are there any other finite fields beside the prime fields? Indeed. For every prime number ‘p’ and whole number ’n’, there is a pⁿ-field called an extension field. Such fields follow different rules of arithmetic than the take-the-remainder approach of prime-fields. And the numbers in such fields are actually polynomials. Let’s take a closer look.

The elements of a pⁿ-field are polynomials of degree n-1 with the coefficients being elements of the prime p-field. For example, the numbers in a 2²-field are polynomials of degree 1 with coefficients in the 2-field. The addition of 2 elements is the addition of the polynomial representations of those elements, with the coefficients added as p-field numbers.

Multiplication of 2 elements in a pⁿ-field is the multiplication of the polynomial representations of those elements, with the coefficients added as p-field numbers. But now the resulting polynomial can be of a degree higher than n-1. To map it back to a pⁿ-field element there is an analogous process to how we took remainders in a prime p-field. In the polynomial case, we divide by any irreducible polynomial of degree n and take the remainder polynomial of degree n-1 as the result. An irreducible polynomial is one that cannot be expressed as the product of 2 other polynomials. In a sense, it is the analog of a prime number that cannot be expressed as the product of 2 smaller numbers.

If representing numbers as polynomials is not exciting enough for you, we can go further. We can represent the numbers in a pⁿ-field as n by n matrices whose elements are p-field numbers. Then, addition and multiplication follow the usual matrix addition and multiplication. What is the matrix representation of the elements? Each n-digit base-p number in the pⁿ-field can be thought of as an n-component vector in an n-dimensional vector space spanned by the n-component vectors (1, 0, …, 0), (0, 1, 0, …, 0), …, (0, 0, …, 0, 1). For example, in the case of the 2²-field, 00 = (0, 0), 01 = (1, 0), 10 = (0, 1) and 11 = (1, 1). Then, the matrix representation of a pⁿ-field element ‘a’ can be constructed in the following way. The first column is the vector corresponding to ‘a’ * ‘00…01’, the second column is the vector corresponding to ‘a’ * ‘00…010’, the third column is the vector corresponding to ‘a’ * ‘00…0100’, and so on.

Summary

1. A field is a set of numbers/elements on which we can do arithmetic (add, multiply, and inversely, subtract and divide).
2. Well-known fields are real numbers and rational numbers. These are infinite fields, that is, they have an infinite number of numbers.
3. For every prime number ‘p’ and whole number ’n’, there is a finite field with pⁿ numbers.
4. If n is 0 then the finite field is a prime field with p numbers: 0, 1, …, p-1. Addition and multiplication proceed as if the numbers are integers. If the result is larger than p-1, then it is divided by p and the remainder is used as the result. Another way to think about this is that the numbers are laid out in increasing order clockwise on a number-circle and addition proceeds by clockwise hops.
5. If n > 0 then the finite field is an extension field with pⁿ numbers: 0, 1, …, pⁿ-1. Arithmetic is done by representing each number as a polynomial of degree < nand coefficients in a p-field. Then, two numbers can be added by adding their polynomials. Similarly, two numbers can be multiplied by multiplying their polynomials. However, the multiplication can yield a polynomial of degree ≥ n. In that case, the polynomial is divided by an irreducible polynomial of degree n, and the remainder polynomial of degree < n is taken as the result. This is analogous to how a result larger than p-1 is handled in a prime p-field. Another way to do arithmetic on pⁿ-field numbers is to use an n by n matrixrepresentation of each number with matrix elements in the p-field. Then, addition and multiplication proceed as usual for matrices.