60 Seconds & 360 Degrees
A Primer on the Sexagemisal System (Base-60)

Have you wondered why there are 60 seconds/minutes in a minute/hour? Or why we decided that a circle is exactly 360 degrees? For the curious cats, it’s likely a common musing that’s piqued your interest at one point or another — our numbering system consistently wraps around ten digits(0–9), except for a few, one-off concepts, why is this?
The short answer is because history intimately ties the proliferation of time & degrees to a period when Base-60, the sexagemisal number system, reigned supreme. The longer answer is this article — where we’ll first introduce the base numbering system, then slowly introduce the Babylonian standard that remains relevant.
What Is A Number Base System?
A base system is a fixed number of different digits, or a combination of digits, that are allowed within a specific numbering system. The universal numbering system, the one you’re most familiar with, is known as the decimal system. The prefix “dec” refers to the nine digits that make up our number system: 0 — 9. In math, instead of saying the decimal system, however, we simply refer to this numbering standard as base-10. While a bit out of scope for this piece, most math-historians theorize that the main reason many societies converged to the decimal system is that we have 10 fingers for counting. To re-state, it’s known as base-10 because the numbering system “wraps around” once the highest digit (9) has been reached.
Either way, the main point is: the decimal number system / base-10 is not the only numbering system (base) that exists. In fact, it’s quite likely that you’ve stumbled across at least one of the following common bases:

It’s this last base system, the sexagemisal base system, that’s the topic du jour. We’ll quickly explain how it works, then dive into the history of why it was established in the first place. Though we’ll review evidence, it’s accepted that no universal answer is agreed-upon, at least for now — we’re only reviewing theoriesbehind the adoption of this powerful remaining base system.
What Is The Sexagemisal (Base-60) System?
As the table above highlights, the sexagemisal system is an ancient numbering system that’s defined by its sixty different digits & is more commonly known as base-60. For reasons we’ll soon cover, the base-60 originated in ancient Sumer in the 3rd millennium BC in Mesopotamia (modern southern Iraq). Soon afterward, it was passed down to the ancient Babylonians & eventually all neighboring nations.
It’s hard to grasp now, but back then the base-60 system was a significant breakthrough in numbering; the fact that it remains relevant in modern, everyday application can’t be overlooked. As the title of the article suggests, base-60 is the numbering system used whenever people tell time or make references to the degrees of a circle.
It’s noticeably distinct in the way it “overflows” from 59 to 0, in contrast to our standard base-10 system. The following table, found in-scripted in Babylonian artifacts, indicates that the vertical wedge (V) represents 1 & the horizontal wedge (<) represents 10 — it is decimal until it reaches 59:

The main fault in the Babylonian system above was the absence of zero — due to this error, 1 & 60 were not distinguishable from their appearance. Distinguishing them from their context was inconvenient & so a sign for blank space was invented shortly afterward.
A second example, slightly chronologically earlier than the table above, the following grid shows the ancient Mesopotamian units of time. One year is divided into 12×30 = 360 days & one day is divided into 12×30 = 360 sub-units. In this example, they actually use base-360 — this was right before the adoption of base-60 but still serves as an example of our notation roots.
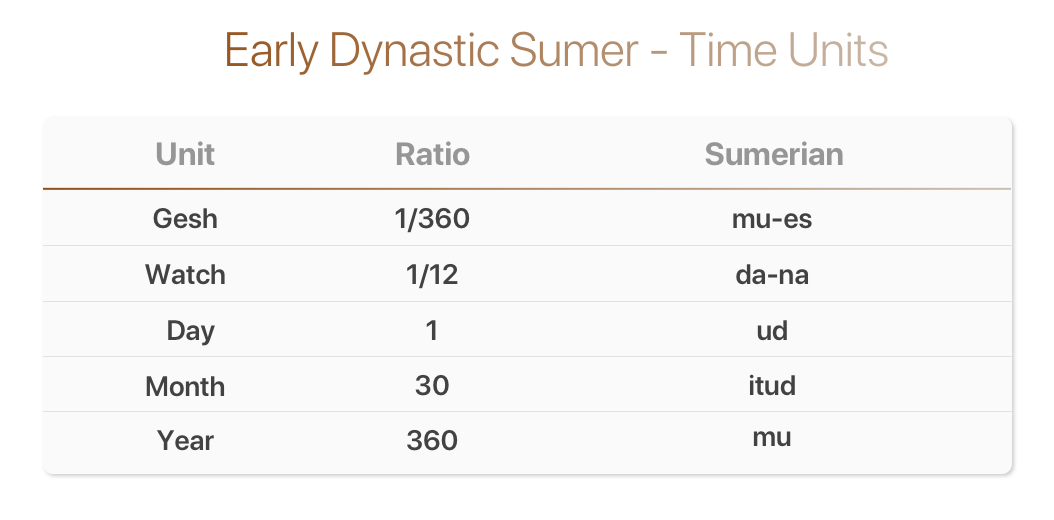
The Sumerians had 12 hours in a day, but at some point, this was changed to 24 hours. Either way, this is one of the earliest-surviving scriptures of an ancient society using an early-sexagemisal system to correspond to time.
But Why Base-60?
Satisfying our curiosity, it’s fair to ask why this base system existed in the first place, or where it came from. Unlike the decimal system, which is almost universally-attributed to the convenience of our ten digits(fingers), the sexagemisal system is a bit more mysterious; there are many competing theories behind this adoption, below, we’ll examine four common hypotheses.
Theory #1 — Cultures Merged
One theory I came across while researching is the following:
The most commonly accepted theory holds that two earlier peoples merged 7 formed the Sumerians. Supposedly, one group based their number system on 5 and the other on 12. When the two groups traded together, they evolved a system based on 60 so both could understand it.
Unfortunately, I was unable to verify the above statement from a legitimate historical source. Many articles out there attribute the quote to a single issue of “USA Today,” yet it appears that the cited issue has disappeared. The basic logic behind this cultural merge, that the Sumerians arrived at Base-60 simply because two preceding cultures used Base-5 & Base-12, seems a bit too convenient without further evidence. Hopefully, it’s now clear why these are simply theories.
Theory #2 — 60 Is A Highly Composite Number
Fortunately, we’re not the first to search through the annals of math history for answers to the rise of Base-60. Famously, the most popular hypothesis proposed was put forth by one Theon of Alexandria. Sometime around the years ca. 335 — ca. 405, he concluded that the Sumerians valued & adopted Base-60 because it has many divisors. To be sure, clocking in at 12 divisors it certainly does have a high amount: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. There are many positive attributes with selecting a number with a high amount of divisors — including that it’s easy to reduce a fraction with 60 its denominator. For further proof that this is likely an intentional choice, take a look at the following table that displays the first 120 numbers with their divisor digits in the y-axis:

A positive integer with more divisors than any smaller positive integer like 60 is called a highly composite number (HCN). HCN goes for a unit of measurement because of its divisibility. As we have already recognized, the ratio between Mesopotamian units of measurement is either a divisor or a multiple of 60.
Theory #3 — 60 Is Also Countable On Our Fingers
As stated in the intro, for the universally-adopted decimal system, there’s a high-consensus among academics & historians as to why it evolved into the most-widely adopted number system — mainly because it’s innate to count to 10 on the fingers of both hands. Following that same train of thought, a third hypothesis attempts to justify the Mesopotamian sexagemisal system with similar logic: a system derived from counting with our digits.
It’s easy to conceive that a base-10 or base-5 system came from counting the fingers of one hand — but how in the world does one count by 12s? As it turns out, it’s unorthodox but entirely possible to count to 12 on one hand. In fact, historian Georges Ifrah argues that the twelve-part numbering system, like the related sixty-part numbering system, goes back to a long-established & widely used finger-counting method. As he puts it, the:
Duodecimal Finger-Counting Method Was Used In India, Indo-china, Pakistan, Afghanistan, Iran, Turkey, Iraq, Syria & Egypt
Despite being un-intuitive to us, it’s clear that the Duodecimal Finger-Counting Method was indeed regionally-popular at one point in time. So how exactly does one count to 12 with our fingers? And how does that tie back into the base-60/sexagemisal system?
Ignoring the thumb, consider the four fingers on your left hand, particularly the three parts split by our two joints. Using our right hand, starting with our thumb, we count these three finger-joints per finger to reach 12. Every time you reach 12, shift over your “counting finger” on your right hand (from thumb, to index to middle…) & continue counting up.
How Does This Reach The sexagemisal (Base-60) Standard? By counting to 12 on our left hand with 5 alternating pointing-instruments (our right hand).
It’s worth noting that no direct, written evidence supports this theory, it’s simply conjecture based on neighboring cultures. And in a way, it’s certainly not a practical counting method, but indeed it’s believable that this mixed finger-counting function was used as a compass to set the numbering-system constraint at 60.
Theory #4 — 60 Has Astronomical Significance
A final theory submitted here suggests an astronomical driver as the main pillar for adoption. A clue to answering why Sumerians had the sexagemisal system lies within their calendar system: the Lunisolar Calendar.
Many neighboring city-states of the Mesopotamians, such as Ur, Uruk & Lagash, all shared the Lunisolar similar calendar. All located near the coastline of the Persian Gulf, this is likely not a coincidence. A geological theory here suggests that they all took considered moon cycles as significant due to the tidal oscillations caused by the Moon’s gravitational pull. This meant heavily prioritizing & adapting the Lunisolar calendar. As the moon phase changes every 30 days (more exactly 29.53), 30 or 29 days must be 1 month.
This checks out with the Sumer time-table presented above. Additionally, we can see from this table that they already marked a year as 360 days. With a need to relate months to years & still fit in with all of the reasons above, it’s a small leap to say that 60 neatly fit this answer as the least common multiple of 12 & 30.
In Closing
We live in an age now compiled with advances by centuries of innovators & academics, we take it for granted, but we’re entirely decoupled from understanding what’s underneath the hood. The internet is ingrained in our lives, yet very few people can explain how it works; millions of people fly every single day, yet less than one passenger per trip can likely explain the physics behind aerodynamics & turbulence.
Our relationship with time & angles is no different. It’s a peculiar anomaly that both concepts use base-60, a slightly different numbering system than the rest of our mathematical language; yet it’s such an intertwined part of our nature, that we now take it for granted without understanding why. And well, at least now you can: the base-60 numbering system is a standard that dates back to the 3rd millennia (BC). Why was it adopted in the first place? There’s no confirmed answer, but four varying theories point to a mix of reasons.





