1988 IMO Question Six

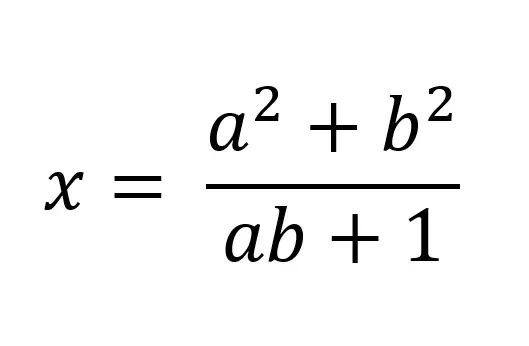
Using no more than high school algebra, here’s how to solve the infamous question 6 from the 1988 International Mathematics Olympiad.

Motivation

This problem has a reputation for being one of the hardest, and perhaps the hardest, IMO problem of all time. And you can solve it only using high school algebra. Struggling through and understanding the solution will do several really cool things for you, but will take time, so motivation is essential.

First, you’ll understand that you can help advance mathematics. I spent several days solving this problem, whereas in the competition they have 4 and a half hours for 3 questions. But I’m not amazing at mathematics — I’m an undergraduate economist. I do maths for fun, and I didn’t give up. You don’t need to be a genius to be a good mathematician. If you work hard, you will be able to solve really hard problems and, maybe one day that will be solving hard research problems. In real life, it doesn’t matter if you are slower than the super geniuses, because there aren’t enough super geniuses to go round. We need ordinary people to work hard and solve problems. Rome wasn’t built in a day, and nor was it built by one person!

Second, you’ll get a taste for what mathematicians do when approaching a problem and the language they use. Normally it takes well into an undergraduate degree to see this because the material is advanced. I have made my solution so that it uses no more than algebra — that’s right, no dreaded calculus or anything! — so that it’s accessible. The solution is then broken down into these things called ‘Lemmas’ and ‘Colloraries’. Lemmas are when we solve a smaller sub-problem which will help solve the big problem. Corollaries are when we look at some implications of using the Lemmas.

The way mathematicians lay things out makes sense. The idea is that we break everything into manageable steps so I, as the problem-solver, can make incremental progress and so you, the reader, can understand every step of the proof. If you can’t understand it, give it a good 10 minutes or so, get pen and paper, and try and figure it out. Ask me in the comments if you’re still stuck, and I’ll reply to you or update my solution to improve the exposition.

Manageable steps is the reason why everyone can work hard and get good at math. If you can’t solve the problem, you play around and solve smaller, perhaps relevant, statements.

I’ll leave exercises throughout. It’s upto you whether or not to use them. If you do use them and work through them, you’ll understand the solution better. If you are stuck on one go back to it a bit later if you aren’t making any progress.

Statement of the problem

IMO proof 1988, question 6

Prove that if x, a, b are all integers then x is a square. For instance, a = 3, b = 27, x = 9 works. So does a = 125, b = 3120, x = 25

Exercise 1. Can you find any other examples of three integers which work? Can you spot any patterns?

Lemma 1

Solutions are paired. Finding one of a pair enables you to find the other.

Imagine you have a list (or ‘set’) of all pairs of integers (x, a).

Doing some algebra, we can see

Exercise 2. Can you work out how I got some or all of these results?

Now we whittle it down to all pairs of integers such that

is a square. Checking the potential even and odd pairings of x and a we can work out that that b will be an integer. (As we are just checking even and odd parities, below I only look at where oddness or evenness results after an operation)

Exercise 3. Why is the square root of an odd number odd? Why is the square root of an even number even? Why is an even number divided by two guaranteed to be an integer?

If we find an (x, a, b) that works, all we need is (x, a) to deduce both values of b which work for those values of x and a. This is because of the +/- in the formula we found for b.

Lemma 2: The Magical Step

There are no solutions where a < 0 and b > 0 (or vice-versa).

This isn’t immediately obvious at all. To start off with, we will rephrase the question. Eyeballing the equation and flipping signs appropriately, you will notice that this is the same as there being positive integers (x, a, b) such that

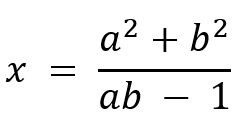
Exercise 4. Can you understand why this is true? (Hint. let a* be < 0 and x* <0, and write a = -a*, x = -x*)

To get a feel of things, let’s get the different ways of looking at this new equation

Exercise 5. Can you verify some or all of these equations?

We first show that, if one of a or b is less than x, then there are no solutions. We show this for a < x, but identical logic can be done to show the b case by symmetry. As we are looking at positive integers (thanks to our rephrasing earlier) we have the following inequalities for x≥3 and a≥4

Exercise 6. The inequality only holds for x ≥3, a≥4. Why might it not be much of a problem that for x = 1,2 and a = 1,2,3 this result doesn’t hold? (Hint. With the original problem, there were an infinite number of possible pairings to check. How many pairings would we have to check to cover these small cases?)

When x = 1 or 2, we can check the original equation by hand for solutions, and same for a = 1,2 and 3, so I’m not concerned much that the inequality doesn’t cover them.

We only have two possibilities for the square value of

These are xa -2 and xa -1. This is because, in Lemma 1, we showed that this value must be an integer. But the inequality only gives to possible integers it could be!

These two values would mean b = 1 or 1/2. The latter is not an integer, and the former is easily checked as xa = 3, so we only have two possibilities to check.

Now comes the magic. If we cannot have either of a or b < x, both are greater than or equal to x. We will show this is a contradiction.

Again, this leaves only a tiny amount of casework, either for us or a computer to check, so I’ll let the reader take the casework on faith rather than making this even longer.

Given this value for a, we pick the smaller solution of b. This must be greater than or equal to x (from our previous reasoning).

This logic is generalised: for every value of a which works, we have now shown it to be greater than 2/3 x², using that for every value of a which work, there are two values of b we can find, and the smaller of those values is greater than x.

Exercise 7. This step is perhaps the most conceptually difficult bit of the solution. Think on it for a bit. Review the pairing of solutions if you need to and the different ways of manipulating our original equation. When you finish the lemma, read it through again.

The ingenious step is then to apply this to b also! But now we know that a ≥ 2/3 x² we can improve our estimate!

As the bound a≥2/3 x² holds for all a, we can prove that, for all b, b≥4/9 x³. But now we can repeat this procedure on a, using our new bound for every value of b.

And we see that, provided x > 3/2, we will get unbounded growth, by pinging back and forth, using our improved bound on a to increase the bound on b, and then use the increased bound on b to increase the bound on a! But this is a contradiction. After all, a and b are finite, but by repeating our procedure we have also shown they are greater than any finite number.

Lemma 3

a,b ≥ root x for all positive integer solutions.

Suppose our arch-nemesis handed us (x, a) such that

Is an integer, and a < root x. Then we write the following as a solution

However, by assumption

This is a contradiction, using lemma 2! After all, we’d have found a solution with a > 0 and b < 0.

Thus both a,b ≥ root x

Lemma 4: The Magical Step revisited

One of a,b < x or one of the paired solutions has one of a*,b* < x

Start with b.

Thus, by assumption, we can deduce

Why? Suppose it were less than x. Then we would be done, as we would have a paired solution with b < x, which is what we wanted.

Now we want to find a suitable lower bound for that horrible square root expression. We have to be quite cunning, to make the inequality tight enough, but not so tight as to lose generality. For x >= 3, we can safely write

Exercise 8. Try and understand why the above inequalities hold.

This allows us to write

As both a and b are greater than x, we also get (by using the same logic with variable names switched)

Thus a > 2x, b > 2x.

But now we can repeat this procedure!!!!!

And we will also be able to deduce that b > 4x. We can repeat this forever. This means there are no solutions, as the lower bound for both a and b can be made arbitrarily large.

Exercise 9. That was hard. Reflect for a bit on why the logic works if you are unsure. Re-read the lemma again now and in a few hours or tomorrow.

Lemma 5

For each solution where neither of a, b <= root x, there exists a paired solution where one of a,b ≤ root x

You hand me a solution where a, b > root x. One of a and b is less than x by Lemma 4. Let’s say it’s a, which gives us the following inequality.

We find a solution b* such that

By the magical lemma, this is a contradiction, or b* = 0, which gives an easy set of cases to verify. (Alternatively, you could use the inequality above to show that there are no integer solutions in the range ax-2a/x and xa which work, as the only option is xa — 1, which can be checked by hand).

Corollary 1

For each solution (x, a, b) there is an implied solution where a = root x or b = root x.

We know that there is an implied solution where one of a or b is <= root x, but we know that neither of them can be less than root x. So, it must be root x

Corollary 2

Corollary 1 solves the question

Root x is an integer in one paired solution. So x is a square.

To avoid confusion, let’s explain this in full.

We can rule out solutions where a < 0 and b > 0 by lemma 2.

We can easily see that solutions where a < 0 and b < 0 are mirrored in solutions where a > 0 and b > 0, as the negative signs cancel.

So we look at positive integer solutions. By lemma 3 there are no solutions where one of a or b is less than root x. (This used lemma 2).

Now we get onto lemma 4. This told us that, given a solution triple (x, a, b) one out of a*, b*, a, b was < x, where a* and b* are the paired or ‘implied’ solutions. Thus, suppose we found all solutions with one of a or b < x had x being a square. Then this would be true for all solutions where both a and b >= x, as x remains the same when we observe the a* and b* this solution is paired with.

Lemma 5 told us that this was indeed true. And so we are done. Can you see how to classify all the solutions? That’s coming next!!

Reflections and thoughts

That was hard. I find it hard sometimes to remember why a bit worked! If you have made it this far, you should feel proud, even if you understand just 10% of what happened. I always feel a bit baffled when I first encounter some hard maths, and it’s only over a long amount of pondering that I ‘get it’.

Exercise 10. Reflect on how well you understood the solution. Spend some time thinking about the bits you found hard, re-read them, write stuff out by hand on paper, ask questions in the comments. If you remember, read through the solution in a few days again, and then in a week or so, and see if you understand more of it.

Math is something to be taken slow. It takes time to digest and understand fully. I often spent days or even weeks mulling over a hard problem.

Free Math Resources

Khan Academy — website with Math, Science and coding, all free. Goes from basics right up to some university level stuff.

3Blue1Brown — Math educator. He creates amazing animated videos to help give an intuitive understanding of math.

Art of Problem Solving — range of math problems, especially competition math.

Past International Maths Olympiad Problems — these are hard. They’re fun to attempt, but be willing to spend a long time working on one.

Dexter’s Notes — Lecture notes and practice sheets from the Cambridge Mathematics Tripos. This is HARD! Not recommended for beginners. Part IA means first year undergraduate, Part IB means second year undergraduate, Part II is third year undergraduate, Part III is fourth year undergraduate / Master’s student.

MIT Opencourseware — Resources, practice exercises and exams from MIT.

I’m a mathematics and philosophy enthusiast, who studies economics at Cambridge University. You can contact me in the comments or via my facebook page. If you want some guidance in how to improve in math, I’d be glad to help!

Edit: 28.08.2020 I’m just updating this article to say I have now succeeded in switching to maths. Yay :)